Shannon entropy

I would like to present the derivation of the Shannon entropy, which is widely used in the Information Theory, based on the concepts of Combinatorics:

• Counting permutations
• From permutations to combinatorial entropy
• From combinatorial to Shannon entropy

Counting permutations

Let's consider the set of balls of different colours: 2 red, 5 green and 3 yellow. Let's consider the pair of the arbitrary alignments of the balls into a line (so-called permutations):

The question is: how many unique permutations are possible, taking into account that the balls of the same colour are non-distinguishable?

If every ball would have it's own unique colour, then the amount of permutations would be 10!, however if there are balls of the same colour - it is possible to mutually exchange them without obtaining of the new permutation.

Hence, in our example we should exclude 5! mutual permutations of the green balls, 3! mutual permutations of the yellow balls and 2! mutual permutations of red ones. So, the amount of the unique permutations in our example would be: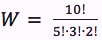

The Multinomial Coefficient is a solution of the general case of described problem: ,

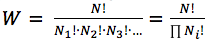where N is a total amount of balls, and N_i is a total amount of the balls of the i-th colour.

From permutations to combinatorial entropy

All permutations can be enumerated and assigned with a number from 0 to (W - 1). Hence, the string of log₂(W) bits can be used to encode each permutation.

As far as each permutation consists of N balls, let's express the average amount of bits per item of the permutation: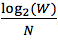

The average amount of bits per item of the permutation is called Combinatorial Entropy:

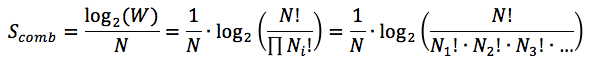
The more uniform set is (the more balls of same colour are there) - the smaller Combinatorial Entropy is, and vice-versa: the more balls of different colours are there - the higher Combinatorial Entropy is.

From combinatorial to Shannon entropy

Let's take a closer look at the expression of the Combinatorial Entropy: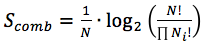

Taking into account the properties of the logarithms, we can transform the expression in the following way:

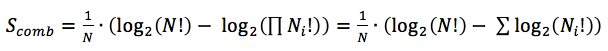
Let's assume that the amount of the items is sufficiently large, so we could make use of the Stirling's formula: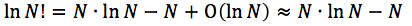

Hence, after application of the Stirling's Formula we get: ,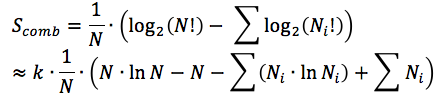

where k - is the transformation coefficient to the natural logarithms.

Taking into account, that 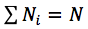we can make the further transformations:

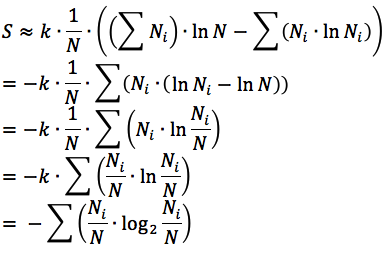
As far as the total amount of balls in a set is N and the amount of balls of i-th colour is N_i - the probability of the random selection of the ball with i-th colour is: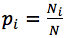

Hence, the entropy can be expressed as: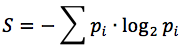

Derived expression is well known as a Shannon Entropy.

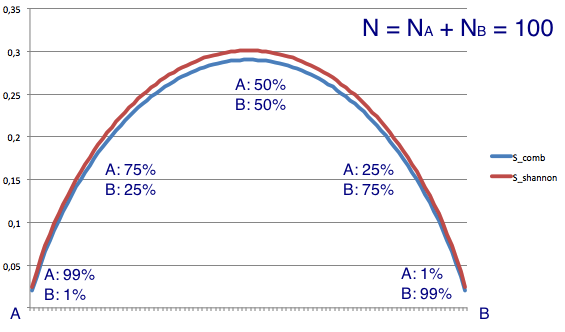
The more tidy derivation could also show that the Shannon entropy is an upper bound of the Combinatorial entropy, hence its value will be always slightly greater than the value of the latter.

Below presented the graph with the comparison of the Shannon and Combinatorial entropies, calculated for the two-item sets (A and B), with a total amount of items N = 100: