Memory-efficient adjacency list implementation technique
While I was solving various problems, which can be reduced to computation on graphs (e.g.: "VOCV - Con-Junctions", "NAJKRACI - Najkraci", "MTREE - Another Tree Problem"), I have discovered a very convenient pattern of implementation of adjacency lists, which I would like to describe in this post.
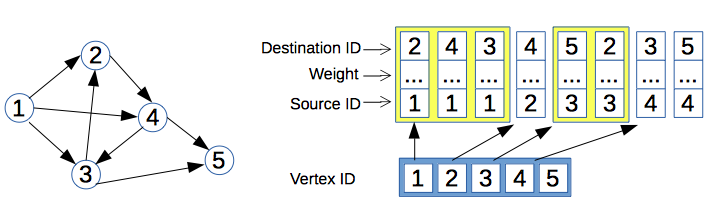
- Motivation
- The commonly used approaches
- The proposed approach
- Example of usage: Breadth-first search
- The full code of the example BFS program
Small remark: sometimes for solving of programming problems I use programming language C (which helps to stay fit in terms of accurate analysis of the problem conditions, tidy memory management, etc.). So, the further snippets of code will be in C, however they can be easily translated to any other programming language.
Motivation
Many graph problems have special limitations, which are known in advance:
- graph is sparse
- amount of vertices does not exceed |V|
- amount of edges does not exceed |E|
- graph is static (consists of a fixed sequence of nodes and edges)
Apart from that, many competitive programming problems have additional requirements:
- execution time limitations
- often it is needed to solve multiple instances of the problem within one run
The need of efficient implementation usually leads to additional limitations, such as:
- the need of avoiding dynamic memory manipulations
- allocation of all required memory at once (on start up of the program)
Actually, the similar requirements and limitations are relevant for some real life problems, which occur in the fields of embedded systems and real-time systems development, etc.
The commonly used approaches
The quick analysis of various sources (e.g.: Wikipedia, Stackoverflow, CLRS (the book of: Cormen, Leiserson, Rivest, Stein)) showed, that it is usually advised to use the linked list based implementation of adjacency lists. And usually, the most straightforward implementation involves the usage of pointers, like this:
typedef
struct {
int dest; // id of a destination vertex
int weight; // weight of an edge
struct Edge * next; // pointer to the next entry of adjacency list
} Edge;
typedef
struct {
int id; // identifier of a vertex
struct Edge * next; // pointer to the first entry of adjacency list
} Vertex;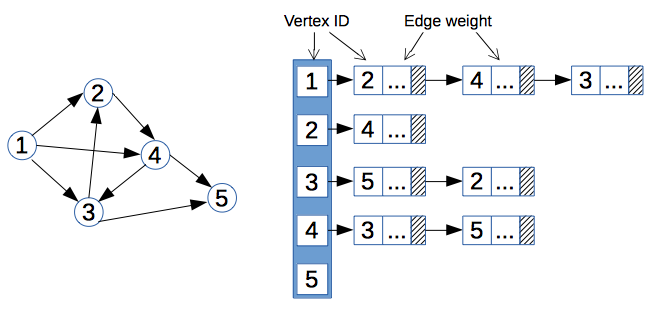
Sometimes, the standard libraries of programming languages provide more convenient data structures, which can be used for implementation of adjacency lists (e.g.: vector in C++, adjacency_list in Boost).
Nevertheless, the described approaches rely on dynamic memory manipulations (allocation of new nodes of the linked list, reallocation of the underlying array of vector).
The proposed approach
Without loss of generality let's assume that each vertex is associated with some unique integer identifier from the interval: [0, |V| - 1].
Let's define a structure, which represents edges of the graph:
typedef
struct {
int from; // id of a source vertex
int to; // id of a destination vertex
int weight; // weight of an edge
} Edge;As far as it is known in advance, that the maximal amount of edges is |E| - at the start up of the program we can allocate an array of size |E|, which can handle all edges of the graph:
#define MAX_EDGES ...
Edge edges[MAX_EDGES];
// amount of edges
// of the current instance of the graph:
int edges_cnt;Let's assume, that array edges is already populated with edges, and the variable edges_cnt indicates an amount of edges of the current instance of the problem. Now, we can sort an array of edges by identifier of a source vertex. It is possible to sort an array with O(E + V) runtime complexity using the Counting Sort:
// auxiliary arrays, allocated at the start up of the program
int vertex_cnt[MAX_VERTICES]; // needed for Counting Sort
Edge edges_sorted[MAX_EDGES]; // sorted edges will be here
// Order edges by id of a source vertex,
// using the Counting Sort
// Complexity: O(E + V)
void sort_edges_by_source() {
// reset the auxiliary data structure
memset(vertex_cnt, 0, sizeof vertex_cnt);
int i;
int key;
int pos;
// count occurrence of key: id of a source vertex
for(i = 0; i < edges_cnt; ++i) {
key = edges[i].from;
vertex_cnt[key]++;
}
// transform to cumulative sum
for(i = 1; i < MAX_VERTICES; ++i) {
vertex_cnt[i] += vertex_cnt[i - 1];
}
// fill-in the sorted array of edges
for(i = edges_cnt - 1; i >= 0; --i) {
key = edges[i].from;
pos = vertex_cnt[key] - 1;
edges_sorted[pos] = edges[i];
vertex_cnt[key]--;
}
}Given the sorted array of edges we can notice, that all outgoing edges of each vertex are grouped together. Hence, using the linear scan over the array of sorted edges - each vertex can be associated with the corresponding position of its outgoing edges:
#define MAX_VERTICES ...
#define NO_OUTGOING_EDGES -1
typedef
struct {
int edges_idx; // index of the first outgoing edge
} Vertex;
// array, indexed by identifier of the vertex
Vertex vertices[MAX_VERTICES];
// amount of vertices
// of the current instance of the graph:
int vertices_cnt;
// Populate each vertex with the corresponding position
// of its outgoing edges.
// Complexity: O(E)
void initialize_vertices() {
int i;
int vertex_id;
for(i = 0; i < vertices_cnt; ++i) {
vertices[i].edges_idx = NO_OUTGOING_EDGES;
}
// first vertex, which has outgoing edges
vertex_id = edges_sorted[0].from;
vertices[vertex_id].edges_idx = 0;
// process the other vertices
for(i = 1; i < edges_cnt; ++i) {
if(edges_sorted[i].from != edges_sorted[i - 1].from) {
vertex_id = edges_sorted[i].from;
vertices[vertex_id].edges_idx = i;
}
}
}Complete graphic illustration of the proposed approach:
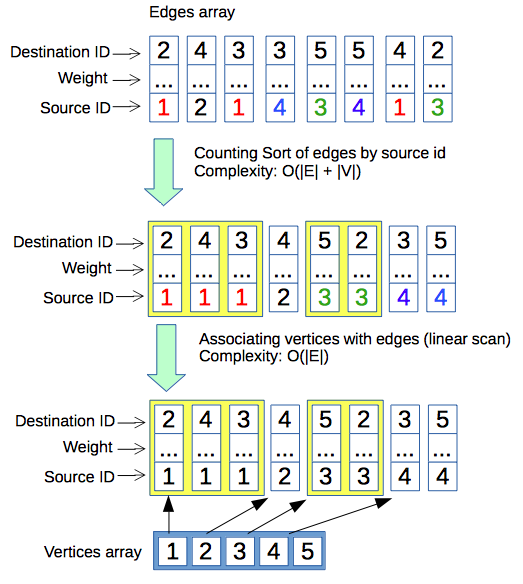
Therefore, the described approach can be used for processing of many different graphs by reusing the same arrays which been allocated only once - at the start of the program. Hence, we can be sure that the program operates within the constant amount of allocated memory.
Additional observation: each bucket of outgoing edges, which belong to the same vertex, can be sorted by identifier of the destination vertex. In this case, we will be able to check the presence of an edge between any pair of vertices with O(log(E)) runtime complexity (using Binary Search).
Of course, described approach is well suitable for problems, which require the computations on static graphs, because the addition of new edges to the packed array of sorted edges is costly.
Example of usage: Breadth-first search
Now, I would like to show the example of usage of given approach, in application to the one of very common graph problems: Breadth-first search (BFS).
As far as the FIFO queue, used in BFS, can't contain more than |V| items - it can be also preallocated at the start up of the program. Below provided a visual explanation of the array based queue:
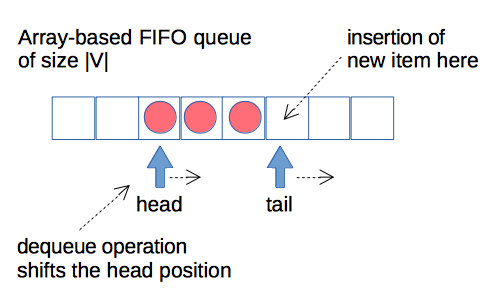
Below provided a code of the BFS, based on the described adjacency list implementation technique and a constant size FIFO queue (the pieces of code, which contain the logic of iteration over the outgoing edges of a vertex are highlighted):
#define TRUE 1
#define FALSE 0
// This array represents the FIFO queue
// of unvisited vertices, and can't be larger
// than the total amount of vertices
int queue[MAX_VERTICES];
// indicates, if vertex already been enqueued into the FIFO queue
int enqueued[MAX_VERTICES];
void bfs(int start_vertex_idx) {
// mark all vertices as not enqueued yet
memset(enqueued, FALSE, sizeof enqueued);
int head; // head of the FIFO queue
int tail; // tail of the FIFO queue
int vertex_idx; // index of dequeued vertex
int edge_idx; // used for iteration over the outgoing edges
int new_vertex_idx; // index of the vertex, which should be visited
// enqueue the index of the start vertex
head = 0;
queue[head] = start_vertex_idx;
enqueued[start_vertex_idx] = TRUE;
tail = 1;
// while queue is not empty
while(head < tail) {
// dequeue the next vertex
vertex_idx = queue[head];
head++;
printf("Visiting vertex: %d\n", vertex_idx);
// process the outgoing edges
edge_idx = vertices[vertex_idx].edges_idx;
if(edge_idx == NO_OUTGOING_EDGES) {
// vertex doesn't have outgoing edges
continue;
}
// iterate over the outgoing edges
while(edges_sorted[edge_idx].from == vertex_idx) {
// destination vertex id
new_vertex_idx = edges_sorted[edge_idx].to;
// if the destination vertex is not yet enqueued
if(!enqueued[new_vertex_idx]) {
// add the destination vertex to the queue
queue[tail] = new_vertex_idx;
tail++;
enqueued[new_vertex_idx] = TRUE;
}
edge_idx++;
}
}
}The full code of the example BFS program
Description of the input data
First line contains the number T, which represents the amount of test cases (amount of different graphs, which are needed to process). Afterwards, follow T blocks with descriptions of the graphs and the source vertices for BFS:
- two numbers V and E, which represent amount of vertices and edges of the current graph
- then, E lines with numbers F and T, which represent the indices of a source and a target vertex
- then, follows a single number, which represents a source vertex for BFS
Example of input data
4
2 1
0 1
02 1
0 1
112 11
0 1
0 2
0 3
1 4
1 5
4 8
4 9
3 6
3 7
6 10
6 11
012 11
0 1
0 2
0 3
1 4
1 5
4 8
4 9
3 6
3 7
6 10
6 11
3
Full code of the solution
#include <stdio.h>
#include <memory.h>
#define TRUE 1
#define FALSE 0
#define MAX_EDGES 100
#define MAX_VERTICES 100
#define NO_OUTGOING_EDGES -1
typedef
struct {
int from; // id of a source vertex
int to; // id of a destination vertex
} Edge;
typedef
struct {
int edges_idx; // index of the first outgoing edge
} Vertex;
Edge edges[MAX_EDGES];
Edge edges_sorted[MAX_EDGES]; // sorted edges will be here
// amount of edges
// of the current instance of the graph:
int edges_cnt;
// array, indexed by identifier of the vertex
Vertex vertices[MAX_VERTICES];
// amount of vertices
// of the current instance of the graph:
int vertices_cnt;
// auxiliary arrays, allocated at the start up of the program
int vertex_cnt[MAX_VERTICES]; // needed for Counting Sort
// auxiliary arrays, allocated at the start up of the program
int vertex_cnt[MAX_VERTICES]; // needed for Counting Sort
Edge edges_sorted[MAX_EDGES]; // sorted edges will be here
// This array represents the FIFO queue
// of unvisited vertices, and can't be larger
// than the total amount of vertices
int queue[MAX_VERTICES];
// indicates, if vertex already been enqueued into the FIFO queue
int enqueued[MAX_VERTICES];
// Order edges by id of a source vertex,
// using the Counting Sort
// Complexity: O(E + V)
void sort_edges_by_source() {
// reset the auxiliary data structure
memset(vertex_cnt, 0, sizeof vertex_cnt);
int i;
int key;
int pos;
// count occurrence of key: id of a source vertex
for(i = 0; i < edges_cnt; ++i) {
key = edges[i].from;
vertex_cnt[key]++;
}
// transform to cumulative sum
for(i = 1; i < MAX_VERTICES; ++i) {
vertex_cnt[i] += vertex_cnt[i - 1];
}
// fill-in the sorted array of edges
for(i = edges_cnt - 1; i >= 0; --i) {
key = edges[i].from;
pos = vertex_cnt[key] - 1;
edges_sorted[pos] = edges[i];
vertex_cnt[key]--;
}
}
// Populate each vertex with the corresponding position
// of its outgoing edges.
// Complexity: O(E)
void initialize_vertices() {
int i;
int vertex_id;
for(i = 0; i < vertices_cnt; ++i) {
vertices[i].edges_idx = NO_OUTGOING_EDGES;
}
// first vertex, which has outgoing edges
vertex_id = edges_sorted[0].from;
vertices[vertex_id].edges_idx = 0;
// process the other vertices
for(i = 1; i < edges_cnt; ++i) {
if(edges_sorted[i].from != edges_sorted[i - 1].from) {
vertex_id = edges_sorted[i].from;
vertices[vertex_id].edges_idx = i;
}
}
}
void bfs(int start_vertex_idx) {
// mark all vertices as not enqueued yet
memset(enqueued, FALSE, sizeof enqueued);
int head; // head of the FIFO queue
int tail; // tail of the FIFO queue
int vertex_idx; // index of dequeued vertex
int edge_idx; // used for iteration over the outgoing edges
int new_vertex_idx; // index of the vertex, which should be visited
// enqueue the index of the start vertex
head = 0;
queue[head] = start_vertex_idx;
enqueued[start_vertex_idx] = TRUE;
tail = 1;
// while queue is not empty
while(head < tail) {
// dequeue the next vertex
vertex_idx = queue[head];
head++;
printf("Visiting vertex: %d\n", vertex_idx);
// process the outgoing edges
edge_idx = vertices[vertex_idx].edges_idx;
if(edge_idx == NO_OUTGOING_EDGES) {
// vertex doesn't have outgoing edges
continue;
}
// iterate over the outgoing edges
while(edges_sorted[edge_idx].from == vertex_idx) {
// destination vertex id
new_vertex_idx = edges_sorted[edge_idx].to;
// if the destination vertex is not yet enqueued
if(!enqueued[new_vertex_idx]) {
// add the destination vertex to the queue
queue[tail] = new_vertex_idx;
tail++;
enqueued[new_vertex_idx] = TRUE;
}
edge_idx++;
}
}
}
// Reads the graph in the following format:
// V E
// F1 T1
// F2 T2
// ...
// Fn Tn
//
// Where:
// V - the amount of vertices
// E - the amount of edges
// Fi, Ti - the i-th edge from the vertex Fi to the vertex Ti
void read_graph() {
scanf("%d %d", &vertices_cnt, &edges_cnt);
int i;
for(i = 0; i < edges_cnt; ++i) {
scanf("%d %d", &edges[i].from, &edges[i].to);
}
}
int main(void) {
// Read the amount of graphs,
// which have to be processed
int tests_num;
scanf("%d", &tests_num);
int start_vertex_idx;
while(tests_num--) {
read_graph();
// read the id of the start vertex for BFS
scanf("%d", &start_vertex_idx);
sort_edges_by_source();
initialize_vertices();
bfs(start_vertex_idx);
printf("\n");
}
return 0;
}Expected output
Visiting vertex: 0
Visiting vertex: 1Visiting vertex: 1
Visiting vertex: 0
Visiting vertex: 1
Visiting vertex: 2
Visiting vertex: 3
Visiting vertex: 4
Visiting vertex: 5
Visiting vertex: 6
Visiting vertex: 7
Visiting vertex: 8
Visiting vertex: 9
Visiting vertex: 10
Visiting vertex: 11Visiting vertex: 3
Visiting vertex: 6
Visiting vertex: 7
Visiting vertex: 10
Visiting vertex: 11
P.S. just in case, the proof of my solutions of the mentioned problems: