I will describe two algorithms for calculation of decimal representation of rational numbers together with recurring decimal (e.g. 1/3 = 0.(3), 3227/555 = 5.8(144), etc.).

Problem analysis

For simplicity let's assume that we have to display recurring decimal always, even if it is equal to zero: 1 / 4 = 0.25(0).

From the school course of Math you might remember, that the procedure of decimal division is just an iterative sequence of integer divisions and calculations of reminder. Below presented the illustration of the first few steps of division process:

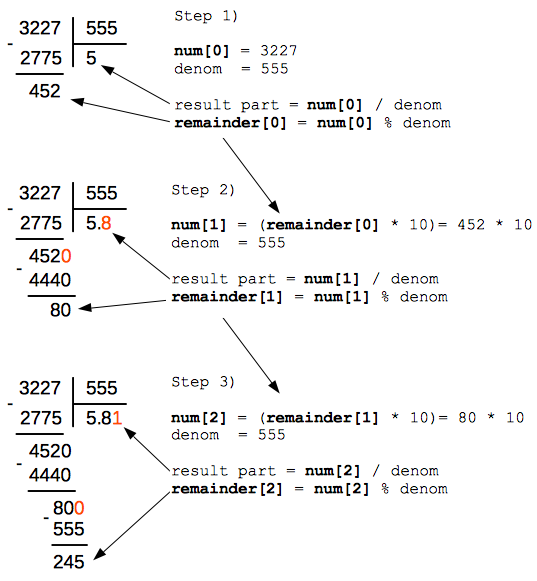
Illustration to the problem

As you might already noticed - the algorithm consists of the series of self-similar steps (starting from the Step 2).

The procedure of repetitive division continues until we reach the same remainder as we already got at some of the previous steps:

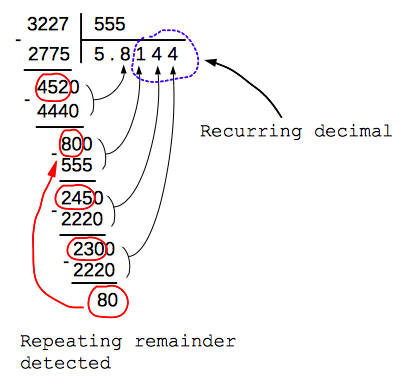
Illustration to the problem

Hence, we can develop the recursive solution of the problem.

Solution with O(N) runtime complexity and O(N) memory consumption

Based on description from above, you can see, that until we reach to the repeating reminder - there is a sequence of unique remainders, which associated with the parts of result.

So, we have to use the data structure, which allows to store the mapping from remainder to result part (preserving the order of insertion), and provides a possibility of fast check - whether any new remainder has been already processed. We can use java.util.LinkedHashMap for given purpose.

Below is provided the snippet of code, with logic of recursive division and collection of remainders (associated with pieces of decimal fraction):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
/** 
 * Returns the first repeating remainder
 */
static int divide(
        int remainder,
        int denom,
        Map<Integer, Integer> remainderToResultPart) {

    // Termination condition:
    // the same remainder has been already processed
    if (remainderToResultPart.containsKey(remainder)) {
        return remainder;
    }

    int num = remainder * 10;

    int resultPart = num / denom;
    remainderToResultPart.put(remainder, resultPart);

    return divide(num % denom, denom, remainderToResultPart);
}

Now, having the recursive routine of division and collection of non-repetitive remainders (associated with decimal fraction parts) - let's implement the rest of functionality (calculation of integer part of division, and output of the final result):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import java.util.LinkedHashMap;
import java.util.Map;

class RecurringDecimal {

    static void divide(int num, int denom) {

        // We have to preserve the order of inserted entities
        // So, let's use LinkedHashMap
        Map<Integer, Integer> remainderToResultPart =
                new LinkedHashMap<>();

        int firstRepeatingRemainder =
                divide(num % denom, denom, remainderToResultPart);

        display(num, denom, firstRepeatingRemainder, remainderToResultPart);
    }

    /**
    * Returns the first repeating remainder
    */
    static int divide(
            int remainder,
            int denom,
            Map<Integer, Integer> remainderToResultPart) {

        // Termination condition:
        // the same remainder has been already processed
        if (remainderToResultPart.containsKey(remainder)) {
            return remainder;
        }

        int num = remainder * 10;

        int resultPart = num / denom;
        remainderToResultPart.put(remainder, resultPart);

        return divide(num % denom, denom, remainderToResultPart);
    }

    static void display(
            int num,
            int denom,
            int firstRepeatingRemainder,
            Map<Integer, Integer> remainderToResultPart) {

        int intPart = num / denom;

        // Display integer part and decimal delimiter
        System.out.print(num + "/" + denom + " = " + intPart + ".");

        for (int remainder : remainderToResultPart.keySet()) {
            if (remainder == firstRepeatingRemainder) {
                // Start of repeating decimal detected
                System.out.print("(");
            }
            int resultPart = remainderToResultPart.get(remainder);
            System.out.print(resultPart);
        }
        System.out.print(")");
        System.out.println();
    }
}

Let's try to execute our code:

1
2
3
4
5
6
7
public static void main(String... args) {
    divide(1, 2);
    divide(1, 3);
    divide(1, 12);
    divide(1, 87);
    divide(3227, 555);
}

You will see the following output:

1/2 = 0.5(0)
1/3 = 0.(3)
1/12 = 0.08(3)
1/87 = 0.(0114942528735632183908045977)
3227/555 = 5.8(144)

Runtime complexity of the algorithm - depends on amount of non-repetitive remainders. So in terms of amount of non-repetitive remainders - complexity of the algorithm is O(N) (where N - represents amount of unique remainders).

As far as we memoize all remainders - memory consumption is O(N) as well. Can we reduce memory requirements somehow?

Solution with O(N) runtime complexity and O(1) memory consumption

We can make use of Floyd's Cycle Detection Algorithm for finding of the first repetitive remainder with O(N) runtime complexity and O(1) memory consumption.

Let's define a class, which represents configuration of the loop:

1
2
3
4
5
6
7
class LoopConfiguration {
    // length of the non-repetitive part
    int preffixLength;
    
    // length of the loop
    int loopLength;
}

Below presented generic implementation of Floyd's Cycle Detection Algorithm:

  • Function<T, T> f - function which generates the next elemnt of a sequence, based on the current element
  • T start - the first elemnt of a sequence
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
static <T> LoopConfiguration detectPreffixLength(Function<T, T> f, T start) {
    T slow = f.apply(start);
    T fast = f.apply(f.apply(start));

    while (!slow.equals(fast)) {
        slow = f.apply(slow);
        fast = f.apply(f.apply(fast));
    }

    slow = start;
    int preffixLength = 0;
    while (!slow.equals(fast)) {
        slow = f.apply(slow);
        fast = f.apply(fast);
        preffixLength++;
    }

    int loopLength = 1;
    fast = f.apply(fast);
    while (!slow.equals(fast)) {
        fast = f.apply(fast);
        loopLength++;
    }

    LoopConfiguration result = new LoopConfiguration();
    result.preffixLength = preffixLength;
    result.loopLength = loopLength;
    return result;
}

Now, having the routine for detection of cycle parameters (length of non-repetitive prefix, and length of the loop) - we can implement the logic for calculation of decimal fraction with repeating decimal:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
static void divide(int nom, int denom) {
    System.out.print((nom / denom) + ".");

    Function<Integer, Integer> div = x -> (x * 10) % denom;
    nom %= denom;
    LoopConfiguration lc = detectPreffixLength(div, nom);

    // Output non-repetitive part of decimal fraction
    for (int i = 0; i < lc.preffixLength; i++) {
        System.out.print((nom * 10) / denom);
        nom = div.apply(nom);
    }

    System.out.print("(");

    // Output recurring decimal
    for (int i = 0; i < lc.loopLength; i++) {
        System.out.print((nom * 10) / denom);
        nom = div.apply(nom);
    }

    System.out.print(")");
    System.out.println();
}

Great side of Floyd's Cycle Detection Algorithm is such, that it consumes O(1) amount of memory, though the runtime complexity is still O(N).