Catch Fish problem from SPOJ: MFISH

Analysis and solution of the problem: http://www.spoj.com/problems/MFISH/

Description of the problem

During his childhood, Mirko liked to play “Sea battle” a lot, but once he got bored of it and invented a new game imaginatively called “Ships catch fish on a river”.

The game board consists of N fields lined up in a row and numbered 1 to N in ascending order from left to right. These fields represent a river on which M ships are to be placed. For each field the amount of fish swimming in that part of the river is known. Every ship has a specific length, i.e. it occupies the specific number of consecutive fields. A ship must somewhere drop an anchor but is allowed to do that in a certain field only. That means that one of the fields a ship will occupy is predetermined.

There can be only one ship or a part of only one ship on a single field of the board. We define the total amount of fish caught as the sum of amounts of fish swimming in all fields occupied by ships. Goal of the game is to place all ships on the river in a way that the total amount of fish caught is maximal.

While playing an instance of this game, Mirko is in doubt whether the way he placed ships is optimal. Therefore asked you to help him calculate the maximum possible amount of fish caught.

Input

First line of the input file contains an integer N, the number of fields on board, 1 ≤ N ≤ 100000.

In the next line there are N integers, separated by whitespaces, which represent the amounts of fish swimming in appropriate field, given in kilograms. These numbers will not be less than 1 nor greater than 100.

The next line contains an integer M, number of the ships, 1 ≤ M ≤ N.

Each of the following M lines consists of two integers B and D separated by a whitespace. That means that the appropriate ship should drop the anchor in a field numbered with B and that its length is D.

Note: input data will always be such that the solution will exist

Output

The only line of the output file should contain the maximum possible total amount of fish caught.

Sample

Input

11
2 5 3 4 7 6 2 1 3 8 5
2
8 3
3 2

Output

20

Input

13
3 2 4 7 2 1 3 6 1 2 6 4 1
2
5 7
11 4

Output

38

Input

11
1 1 6 4 4 1 1 3 10 1 1
3
2 3
6 4
10 2

Output

31

Understanding the problem

Below provided a graphical representation of the problem's description:

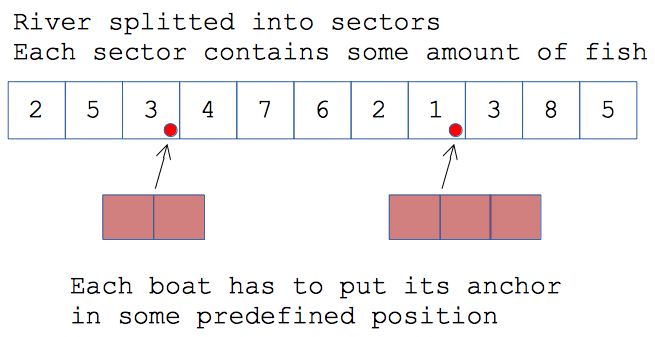
Illustration to the problem

Each boat has to put its anchor, strictly, into its own position. Positions of anchors are fixed - which means, that at least one segment of every boat has to be located in segment of the river with a boat's anchor.

Apart from that - it is possible to vary alignment of the boats (boats are not allowed to overlap). Each alignment can be characterized by total coverage of fish.

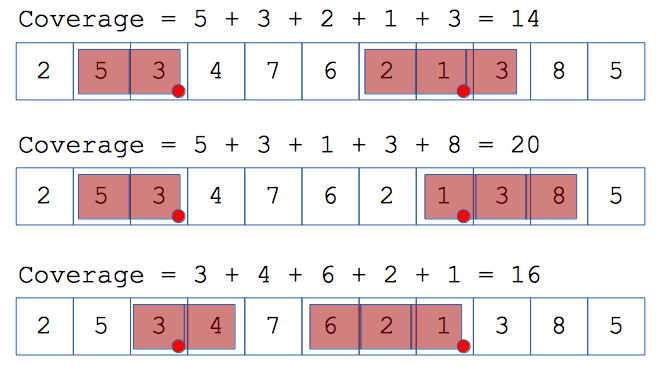
So, we have to find the largest possible coverage of fish (with respect to predefined anchor positions, and lengths of the boats). Below presented few possible alignments of the boats:

Example of alignments

Modelling the problem

The river can be modelled just by simple array int[] fish - where each cell represents amount of fish in corresponding location (according to problem's description, indexing of positions starts from 1, in contradiction to commonly used 0-based indexing in arrays - so we have to be careful).

For convenience, let's define class, which represents boat:

class Boat {
    int anchor;
    int length;

    // let's introduce a variable, which represents
    // the leftmost allowed position of the boat
    int minPos;

    Boat(int anchor, int length) {
        this.anchor = anchor;
        this.length = length;
        this.minPos = (anchor - length) + 1;
        if (this.minPos < 1) {
            this.minPos = 1;
        }
    }
}

So, we have to develop some function, which returns the largest possible coverage for given array of boats and array of fish amounts:

static int solve(int[] fish, Boat[] boats) {
    // ...
    // Our algorithm will be here
    // ...
    return result;
}

As far, as description of the problem does not tell anything about the order of the boats inside input data - let's sort the boats by location of anchors:

static int solve(int[] fish, Boat[] boats) {
    Arrays.sort(boats, (b1, b2) -> Integer.compare(b1.anchor, b2.anchor));
    // ...
    // Our algorithm will be here
    // ...
    return result;
}

After analysis of restrictions of the problem (boats can't overlap, and must be connected with their anchors), we can notice an important insight about the problem: (after sorting boats by anchor location) - the precedence order of the boats will be fixed for any possible alignment of boats.

Brute force solution

Let's look closer into the instance of our problem, and try to trace the possible solution of the problem:

imagine, that we put the 1st boat into some feasible position x (such that distance to its anchor is smaller than length of the boat: (x + boats[1].length) >= boats[1].anchor)
now, we must put 2nd boat into its feasible position y - and, with respect to restrictions of our problem (boats can't overlap), we have to choose such y, that y > (x + boats[1].length)
now, we have to put 3rd boat into its feasible position z, such that
z > (y + boats[2].length)
and so on...

So, we can see that steps of our solution are very similar, and we just have to:

track the index of the current boat: b
track the first feasible position for curent boat on the river: s (such position, which doesn't overlap with previous boat)

Based on the observations from above - we can represent the solution of the instance of problem, through solutions of smaller subproblems:

Recurrence relation

Let's simplify our recurrence relation a bit. To do this, let's consider two possible ways of implementing the function, which finds the maximum value inside array:

Iterative:

static int max(int[] arr) {
    int result = Integer.MIN_VALUE;
    for(int i = 0; i < arr.length; i++) {
        result = Math.max(result, arr[i]);
    }
    return result;
}

Recursive:

static int max(int[] arr) {
    return max(arr, 0);
}

static int max(int[] arr, int i) {
    if(i == arr.length) return Integer.MIN_VALUE;
    return Math.max(arr[i], max(arr, i + 1));
}

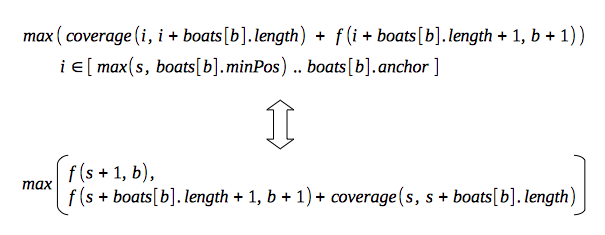
Recursive implementation allows to get rid of explicit loop routine, hence the same approach can be used for simplification of our recurrence relation. So, the following expressions are equivalent: Loopless recurrence formula

So, our final recurrence relation is following:

Below presented recursive solution, which is based on recurrence relation from above:

import java.util.Arrays;

public class MFISH {

    static int solve(int[] fish, Boat[] boats) {
        Arrays.sort(boats, 
                    (b1, b2) -> Integer.compare(b1.anchor, b2.anchor));
                    
        int result = solve(boats, fish, 1, 0);
        return result;
    }

    static final int NEGATIVE_INFINITY = -100000000;

    static int solve(Boat[] boats, int[] fish, int start, int boat) {

        if (boat == boats.length) {
            // all boats successfully aligned
            return 0;
        }

        if (start > boats[boat].anchor) {
            // anchor of the boat is unreachable
            // from given start position
            return NEGATIVE_INFINITY;
        }

        if (((fish.length - start) + 1) < boats[boat].length) {
            // boat can't fit into the river 
            // (intersects the right boundary of the fish array)
            return NEGATIVE_INFINITY;
        }

        if ((start + boats[boat].length) <= boats[boat].anchor) {
            // given start position is too far from
            // anchor of current boat
            // so, the start position has to be closer
            return solve(boats, fish, start + 1, boat);
        }

        int subProblem1 = solve(boats, fish, start + 1, boat);

        int coverage = 
                countFish(fish, start, (start + boats[boat].length) - 1);
                
        int subProblem2 = coverage +
                solve(boats, fish, start + boats[boat].length, boat + 1);

        return Math.max(subProblem1, subProblem2);
    }

    static int countFish(int[] fish, int from, int to) {
        int coverage = 0;
        for (int i = from - 1; i <= (to - 1); i++) {
            coverage += fish[i];
        }
        return coverage;
    }
}

Dynamic Programming solution with O(N * M) complexity

We can notice that solution of every subproblem depends only on two variables:

s - position in the river
b - index of current boat

Based on the information from the problem's description - we can see, that there are only N possible values of s, and only M possible values of b.
Hence, there are only M * N possible combinations of s and b (let's call them - states).

So, we can make use of Memoization technique - in order to transform brute force solution into Top Down Dynamic Programming solution. Below presented code, which is very similar to the previous one - but, additionally, augmented with logic for memoization (highlighted lines of code):

import java.util.Arrays;

public class MFISH {

    static int solve(int[] fish, Boat[] boats) {
        Arrays.sort(boats, 
                    (b1, b2) -> Integer.compare(b1.anchor, b2.anchor));

      int[][] memoized = new int[fish.length + 1][boats.length];
       for (int[] row : memoized) {
           Arrays.fill(row, NOT_INITIALIZED);
       }

        int result = solve(boats, fish, 1, 0, memoized);
        return result;
    }

    static final int NEGATIVE_INFINITY = -100000000;
    static final int NOT_INITIALIZED = -1;

    static int solve(Boat[] boats, int[] fish,
            int start, int boat,
          int[][] memoized) {

        if (boat == boats.length) {
            // all boats successfully aligned
            return 0;
        }

        if (start > boats[boat].anchor) {
            // anchor of the boat is unreachable
            // from given start position
            return NEGATIVE_INFINITY;
        }

        if (((fish.length - start) + 1) < boats[boat].length) {
            // boat can't fit into the river
            // (intersects the right boundary of the fish array)
            return NEGATIVE_INFINITY;
        }

      if (memoized[start][boat] != NOT_INITIALIZED) {
           return memoized[start][boat];
       }

        if ((start + boats[boat].length) <= boats[boat].anchor) {
            // given start position is too far from
            // anchor of current boat
            // so, the start position has to be closer
            return solve(boats, fish, start + 1, boat, memoized);
        }

        int subProblem1 = solve(boats, fish, start + 1, boat, memoized);

        int coverage = 
                countFish(fish, start, (start + boats[boat].length) - 1);
                
        int subProblem2 = coverage +
        solve(boats, fish, start + boats[boat].length, boat + 1, memoized);

      memoized[start][boat] = Math.max(subProblem1, subProblem2);
       return memoized[start][boat];
 }

    // This method can be implemented with O(1) complexity,
    // using cumulative sum array
    static int countFish(int[] fish, int from, int to) {
        int coverage = 0;
        for (int i = from - 1; i <= (to - 1); i++) {
            coverage += fish[i];
        }
        return coverage;
    }
}

Provided code - contains implementation of method countFish with O(N) runtime complexity. But, actually, calculation of amount of fish on the interval - can be done with O(1) runtime complexity, using cumulative sum array (see: Counting boat coverage with O(1) complexity). So, for now, let's assume that runtime complexity of method countFish is O(1).

Hence, runtime complexity of each recursive step is O(1) - algorithm performs constant amount of opertaions. The total amount of states is M * N - so, overall complexity of solution is O(N * M).

To avoid the overhead of recursive calls mechanics (memory frame allocations), povided algorithm could be transformed into Bottom Up Dynamic Programming solution.

Unfortunately, the boundary conditions of the problem are pretty big: M <= N <= 100000 - so, our O(M * N) solution is not sufficient for the instances of problem with large M and N.

Can we do better?

Dynamic Programming solution with O(N) complexity

Additional analysis of the problem

Let's analyze the set of possible locations of the leftmost border of each boat. Below presented the illustration, which helps to disclose the useful insight about the problem:

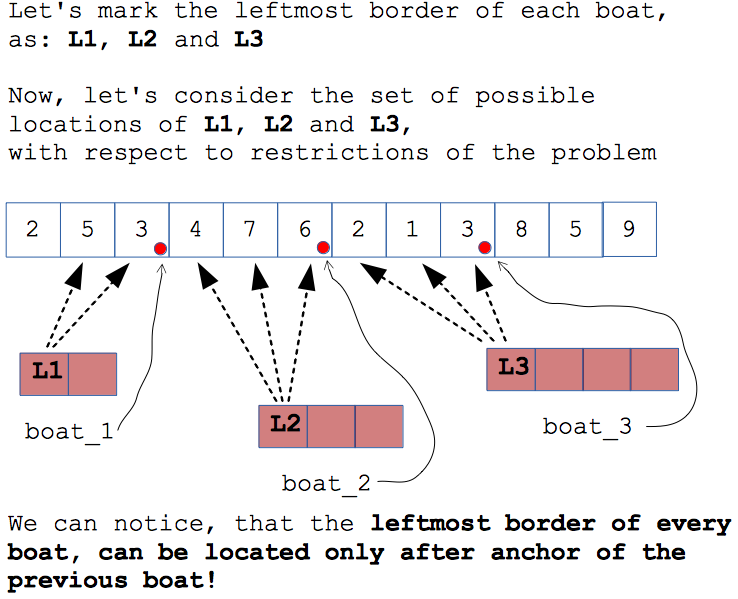
Analysis of location of the leftmost borders of the boats

Which implies, that there is 1:1 relation between position on the river - s, and index of boat - b, which can start at given position!

Formally speaking, it means that b = g(s) - index of the boat is just a function of the position on the river (b can be derived from given position on the river - s).

As far as variables, which represent state (b and s) are not independent - we can get rid of redundant variable:

Enhanced recurrence relation

So, as you can see - the state, which represents partial solution of the problem depends only on variable s. As far as there are only N different values of s - we have to solve only N different subproblems, in order to find the optimal solution.

O(N) algorithm

Below presented Top Down Synamic Programming solution with O(N) complexity:

import java.util.Arrays;

public class MFISH {

    static int solve(int[] fish, Boat[] boats) {
        Arrays.sort(boats,
                (b1, b2) -> Integer.compare(b1.anchor, b2.anchor));
      // We have to memoize only O(N) solutions of subproblems!
       int[] memoized = new int[fish.length + 1];
     Arrays.fill(memoized, NOT_INITIALIZED);

        // Get 1:1 mapping of river segments -> to boat indices
      int[] boatIndices = getBoatIndicesMapping(fish, boats);

        int result = solve(boats, fish, 1, boatIndices, memoized);
        return result;
    }

    static final int NEGATIVE_INFINITY = -100000000;
    static final int NOT_INITIALIZED = -1;
    static final int NO_BOAT_CAN_BE_HERE = -1;

    static int solve(Boat[] boats, int[] fish,
            int start,
          int[] boatIndices,
           int[] memoized) {

        // get index of current boat (from 1:1 mapping)
      int boat = boatIndices[start];

      if (boat == NO_BOAT_CAN_BE_HERE) {
         // in case, if no boat can be aligned
            // in the current segment of the river
          return NEGATIVE_INFINITY;
     }

        if (boat == boats.length) {
            // all boats successfully aligned
            return 0;
        }

        if (start > boats[boat].anchor) {
            // anchor of the boat is unreachable
            // from given start position
            return NEGATIVE_INFINITY;
        }

        if (((fish.length - start) + 1) < boats[boat].length) {
            // boat can't fit into the river
            // (intersects the right boundary of the fish array)
            return NEGATIVE_INFINITY;
        }

        if (memoized[start] != NOT_INITIALIZED) {
            return memoized[start];
        }

        if ((start + boats[boat].length) <= boats[boat].anchor) {
            // given start position is too far from
            // anchor of current boat
            // so, the start position has to be closer
            return solve(boats, fish, start + 1, boatIndices, memoized);
        }

      int nextBoatIndex;

        // Subproblem 1
        // we would like to check the gain, in case if we put current boat
        // into the next position on the river
      nextBoatIndex = ((start + 1) < boatIndices.length)
               ? boatIndices[start + 1]
               : NO_BOAT_CAN_BE_HERE;
       int subProblem1 = (nextBoatIndex == boat)
             ? solve(boats, fish, start + 1, boatIndices, memoized)
                : NEGATIVE_INFINITY;

        int coverage =
                countFish(fish, start, (start + boats[boat].length) - 1);

        // Subproblem 2
        // we would like to check the gain, in case if we put current boat
        // into the current position on the river
        // (the index of next boat should differ by 1 - from the index of current boat)
      nextBoatIndex = ((start + boats[boat].length) < boatIndices.length)
               ? boatIndices[start + boats[boat].length]
               : NO_BOAT_CAN_BE_HERE;
       int subProblem2 = (nextBoatIndex == (boat + 1))
             ? coverage + solve(boats, fish, start + boats[boat].length, boatIndices, memoized)
                : coverage;

        memoized[start] = Math.max(subProblem1, subProblem2);
        return memoized[start];
    }

    // Calculating 1:1 mapping with O(N) complexity
    // from the index of river segment
    // to the index of boat, which can start at given segment
  static int[] getBoatIndicesMapping(int[] fish, Boat[] boats) {
       int[] boatIndices = new int[fish.length + 1];
       Arrays.fill(boatIndices, NO_BOAT_CAN_BE_HERE);

       int currBoatIdx = 0;
       for (int i = 0; i < boatIndices.length; i++) {
           boatIndices[i] = currBoatIdx;

           if (boats[currBoatIdx].anchor == i) {
               currBoatIdx++;

               if (currBoatIdx == boats.length) {
                   break;
               }
           }
       }

       return boatIndices;
   }

    // This method can be implemented with O(1) complexity,
    // using cumulative sum array
    static int countFish(int[] fish, int from, int to) {
        int coverage = 0;
        for (int i = from - 1; i <= (to - 1); i++) {
            coverage += fish[i];
        }
        return coverage;
    }
}

Now, our O(N) solution can handle even large instances of the problems (when N around 100000). For purpose of the further optimization (to avoid memory frame allocations on a stack) - given solution can be transformed to Bottom Up Dynamic Programming algorithm (we will need to traverse river's segments from right to left).

Actually, you might already notice, that at the first step of our algorithm - we sort our boats (default implementation of sorting algorithm in Java has runtime complexity O(N * log(N))). But, actually, we can sort all boats with O(N) runtime complexity (see: Sorting boats with O(N) complexity).

Other optimizations

Counting boat coverage with O(1) complexity

We can use Cumulative sum array technique for counting fish, which covered by boat with O(1) runtime complexity.

Initially, we have to precalculate prefix-sum array:

// Precalculate cumulative sum array - complexity O(N)
int[] cumulativeSumArray = new int[fish.length + 1];
cumulativeSumArray[0] = 0;
for (int i = 1; i < cumulativeSumArray.length; i++) {
    cumulativeSumArray[i] = cumulativeSumArray[i - 1] + fish[i - 1];
}

Afterwards, we can use prefix-sum array - for calculation of elements sum on given interval:

// Complexity is O(1)
static int countFish(int[] cumulativeSumArray, int from, int to) {
    return cumulativeSumArray[to] - cumulativeSumArray[from - 1];
}

More useful information can be found here: http://wcipeg.com/wiki/Prefix_sum_array_and_difference_array

Sorting boats with O(N) complexity

As far as we know limits of our problem: N <= 100000 - we can use Counting sort to sort boats with O(N) runtime complexity.