Posts
-
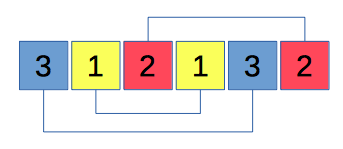
In combinatorial mathematics, a Langford pairing, also called a Langford sequence, is a permutation of the sequence of 2n numbers (1, 1, 2, 2, ..., n, n) in which the two ones are one unit apart, the two twos are two units apart, and more generally the two copies of each number k are k units apart. Langford pairings are named after C. Dudley Langford, who posed the problem of constructing them in 1958.
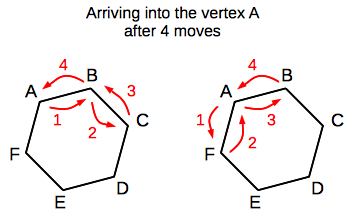
There is a hexagon and a traveller, which moves between vertices of the hexagon. At every step the traveller randomly chooses one of adjacent vertices and moves there. The question is: how many paths are there - which end in the initial vertex after N steps?
For the sake of convenience, let's assign letters to the vertices of the hexagon, and let's assume that initial vertex is "A". Below is an illustration, which demonstrates two paths (out of six possible), which end in the initial vertex after four steps (the arrows are indexed in the order of performed moves):
I will describe a couple of algorithms for tackling described problem, we will see how the runtime efficiency of solutions can be improved from an exponential complexity down to almost a constant time complexity. And, finally, we will discuss the pros and cons of each approach.
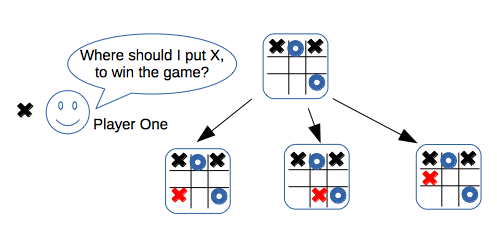
This article contains a brief introduction of the Minimax principle, together with minimalistic and pure functional implementation of the Minimax algorithm in Scala for the purpose of creation of the unbeatable Tic-Tac-Toe program.
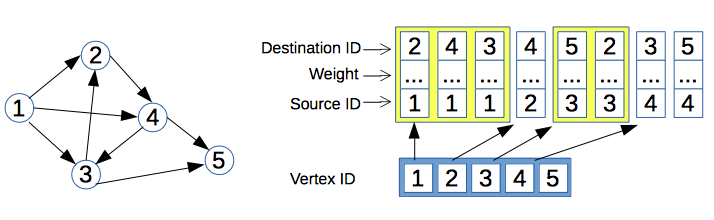
While I was solving various problems, which can be reduced to computation on graphs (e.g.: "VOCV - Con-Junctions", "NAJKRACI - Najkraci", "MTREE - Another Tree Problem"), I have discovered a very convenient pattern of implementation of adjacency lists, which I would like to describe in this post.
I would like to present the derivation of the Shannon entropy, which is widely used in the Information Theory, based on the concepts of Combinatorics:
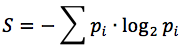
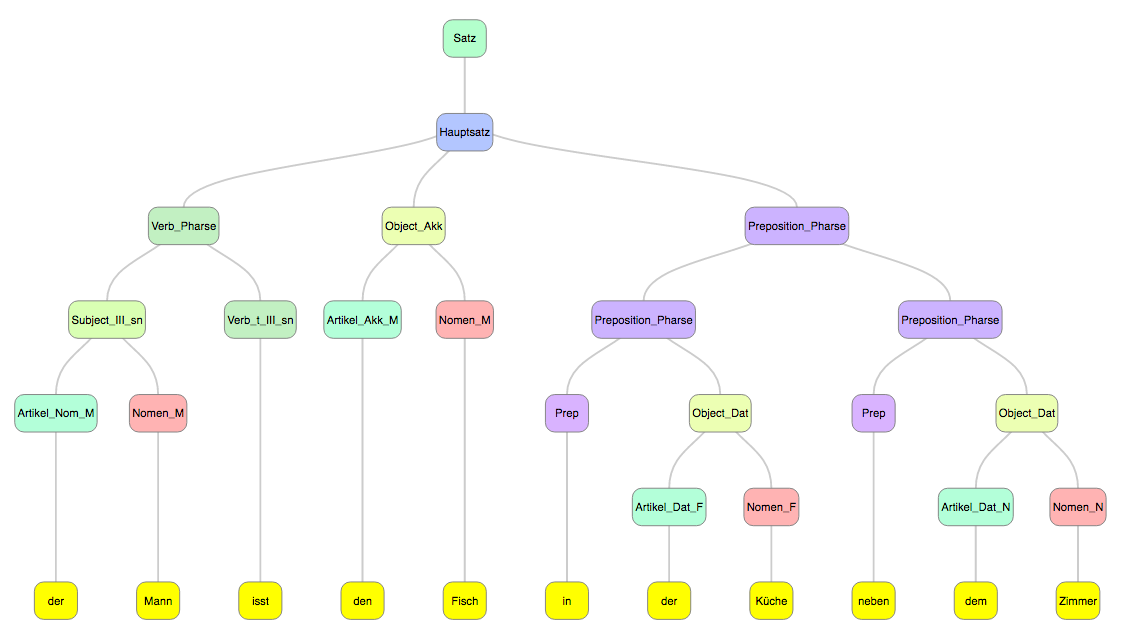
I have combined the process of learning German with my hobby, and would like to present the prototype of the parser of the subset of German language.
We will use the Pumping Lemma, in order to understand whether it is possible to describe the prime numbers using a Regular Grammar.
I will describe two algorithms for calculation of decimal representation of rational numbers together with recurring decimal (e.g.
1/3 = 0.(3),3227/555 = 5.8(144), etc.).